Trying AlphaZero on Some Combinatorial Games
One lazy thing to do when you want to try and learn a few things is to smash them all together. It is probably suboptimal but it is something of a time-saver. I had a desire to get familiar with Julia, to understand AlphaZero a little better, and to get familiar with some aspects of combinatorial games, so why not train a model to play a combinatorial game or two?
Current status: implemented a bad version of AlphaZero in Julia using the monkey-see-monkey-do method (monkey saw a tutorial+repo and a different Julia implementation). Working through some BatchNorm instability and figuring out if monkey did what monkey saw correctly. Will need to compare against the referenced existing implementations and troubleshoot. May wind up just using one of those two once I feel that I “get it.”
Current status (5/30ish): Coming back to this after being busy w/ some work. Still figuring out what I am doing wrong w.r.t. BatchNorm. I’m thinking I did something stupid and obvious (only in retrospect of course). Going to use a canned library after some more wrestling as I am pretty eager to poke at the policies learned for some combinatorial games. I can always circle back to implementation.
~~5/31: Some lunchtime fiddling. Left this thing to run (on CPU…) last night while out. Seems to always be selecting k = 1 in the (modified) Euclid game I have set up. I might have implemented something wrong, but I have read that people have issues centered around finding the correct \(c_{puct}\) constant value. Going to let it rip with \(c_{puct}\) = 5 and see if that improves anything. Otherwise going to compare (again) what I implemented to one of those other libraries to see if that points me toward an answer (incl. re: BatchNorm instability). ~~
5/31-6/20ish: Went back 5/31 or 6/1 and just removed the BatchNorm piece for now. Also corrected some stupid update I was doing in an inner loop and sped up training quite a bit. Policies are no longer total nonsense. After these changes haven’t really touched anything for a few weeks, didn’t have the time. Have about 30 min today. Want to start looking at how the network plays relative to optimal play.
6/26: When the network plays itself, players A and B seem to have ~equal win rates, close to 50%. But player A should have a win rate close to 61.8%. The question now is: did I implement anything wrong, do I need to train for much longer or on more examples, or does this network have some trouble with this type of combinatorial game? As far as implementation, I’m sure something is off since I don’t trust myself, but since it’s late and I am tired we’ll have to return to that theory. As far as training for much longer or on more examples, that’s something I can get running right now, and then head off to bed and look at the results of tomorrow.
6/27-6/30ish: I made the network significantly smaller (layer 1 from 1024 down to 32, layer 2 from 512 down to 16). I have no idea why I was training a broad network, I guess I just thought a big number seemed cool (I do not really do much deep learning in my day job or in my previous knock around projects). I still have no BatchNorm and I’ve also temporarily taken away any self-play steps in the AZ implementation (the part where two networks are pitted against one another and you only take the newest one if the win rate is greater than some threshold). Trying to keep everything as simple as possible until I have some idea what’s up.
7/1: Policy loss was starting to spontaneously comubst. Realized I was taking the log of some 0s so I am just uniformly adding 1e-35 jsut before taking the log to avoid that. Plotting the value estimates for all 1-100 pairings doesn’t exactly look promising but it definitely looks not discouraging.
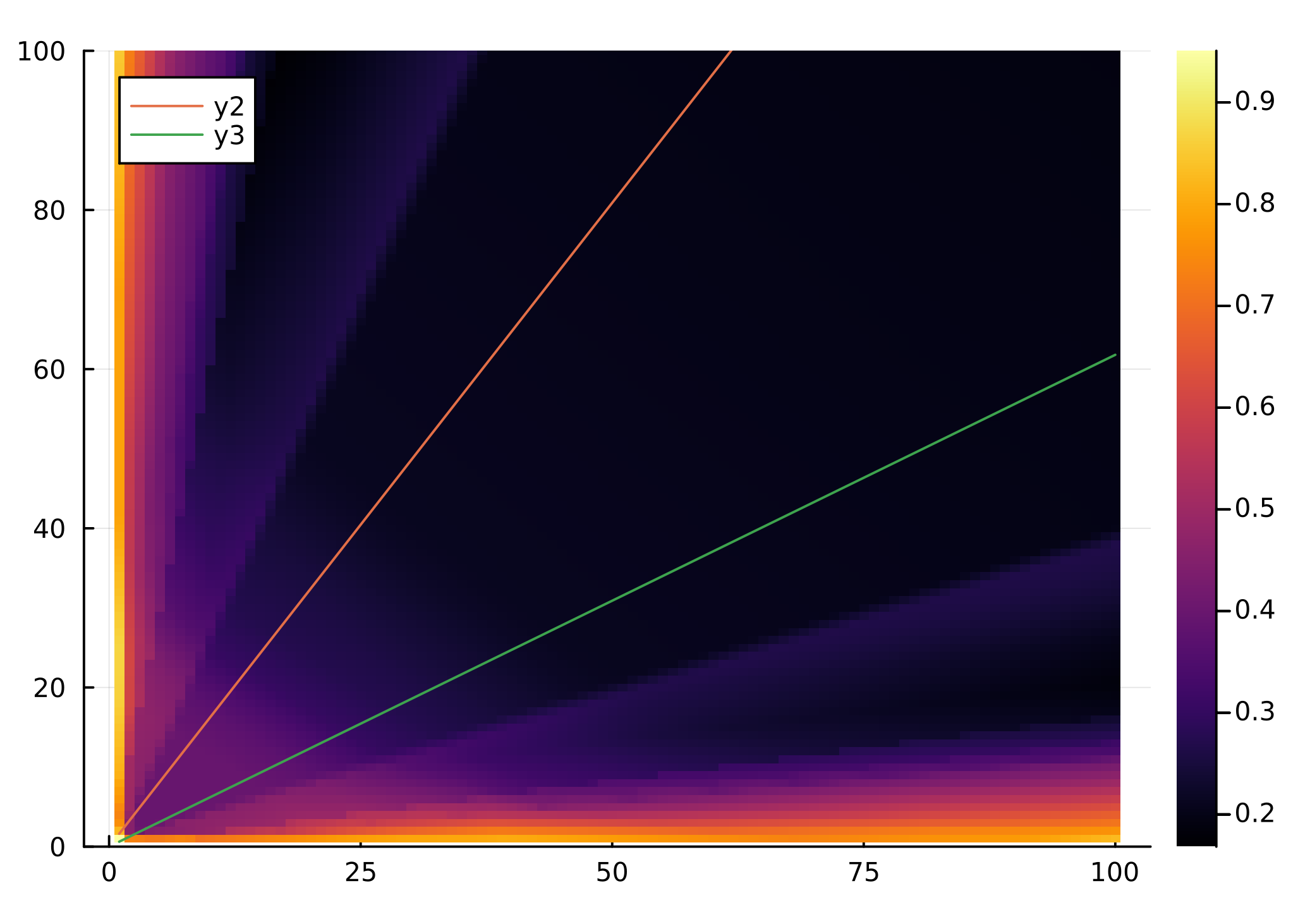
7/1 evening: I think the network is stuck in some sort of local minima. Loss just plateaus. Maybe I should try changing the learning rate or introducing a bit more exploration?
7/2: Ahhhhhh. I wasn’t tracking which player’s turn it was… I reintroduced the self-play step, but I may need to take it back out for the time being. The threshold is pretty unforgiving if the network performs like garbage, which does seem to happen a lot early on. That means a lot of wasted training. I’m trying to give more examples in a pass first.
7/3: Okay, fixed those issues. Took the self-play back out – it’s hard to say just what a “sensible” win-rate is for this game, and for quite some time I was just throwing away every round of training. I also started allowing for the saving & loading of the MCTS data, as throwing it away and starting fresh each run seems imprudent if not outright incorrect. The handy tutorial points out that in the original AlphaGo paper the policy taken after MCTS is eventually turned greedy after about 30 “moves” in the game – I was not doing this, so I made that change. Doing a nice long run, let’s see if the value estimates start looking more like what would be implied by the optimal strategy. I dropped c_puct back to 1. There really are a lot of hyperparameters flying around in deep RL, and I assume this is a mild case. I haven’t been very rigorous about all my changes. My intent is to train something that looks about right, and then I can backtrack and do everything from scratch across with rigorous change tracking. If I do get half-decent performance here, I’d love to get my feet wet with some “mechanistic interpretability” ala Acquisition of Chess Knowledge in AlphaZero.
7/4-7/8: Cloned the alpha-zero-general repo and tried implementing the game of Euclid there (Python & PyTorch). I’d like to compare training results. I’d also like to sanity check my MCTS vs the one in there by running a few pairs of numbers through each search procedure. My very light literature search seems to indicate that deep RL doesn’t often perform well on Nim-variants/combinatorial games, but I need to be really certain there is no issue in my current implementation to pursue this. I saw a few papers/theses that used tabular methods on Nim(-variants) with success, so it might be prudent to sub in something like that in place of the policy/value network (maybe some kind of Monte Carlo control method would do? Or really simple policy iteration? I have some Sutton & Barto exercises I can repurpose here so that’d be the prudent/lazy choice).
7/9: I wasn’t masking invalid moves, I was making invalid moves lead to a loss. My theory as to why that is bad is that it means “wait for my opponent to do something really stupid” could become a valid strategy to learn – or more like “I can learn an arbitrary strategy so long as my opponent does something stupid next move.” E.g. say we start with (4, 12). Player 1 ought to play 3 and win at (4, 0), but when we don’t mask illegal moves who’s to say it’s wrong to play e.g. 1 if player 2 might play 8 and you win anyway? Without thinking too deeply, I’d think this would make learning pretty difficult (inefficient?) since there are all sorts of advantageous positions that could get totally blown up. Eventually we should still expect to see low probabilities assigned to these illegal actions, but we’re total noobs and training on CPU here so let’s not push our luck, eh?
Also realized the self-play aspect is meant to use MCTS as well (duh). Self-play doesn’t seem to add much for the game of Euclid. Constantly just throwing away networks. One could also frame that as “freshly trained networks don’t improve much,” but how do we know the network isn’t just one prod or jostle away from some interesting point in the landsacpe? I’ll keep tinkering either way.
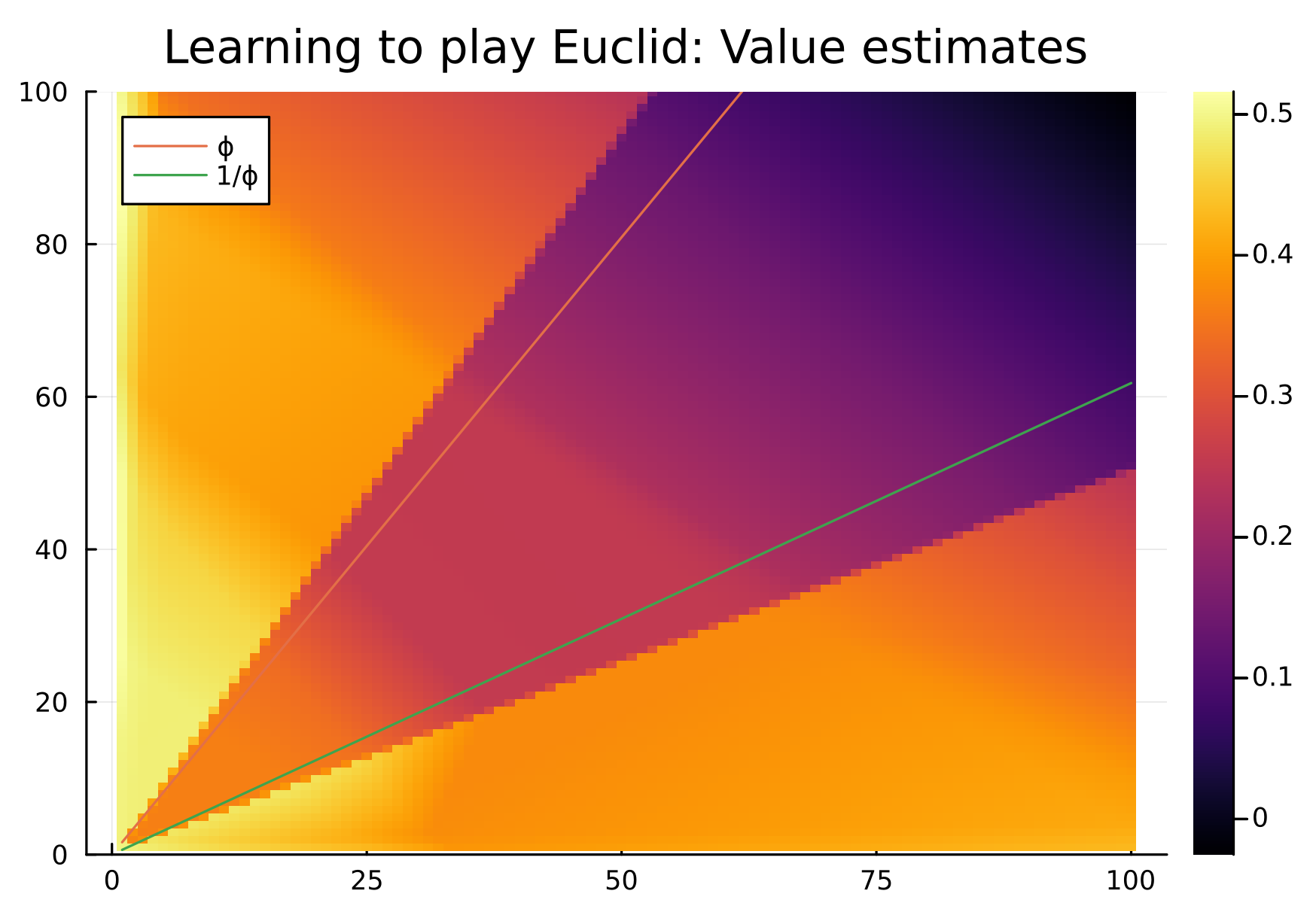
Here’s yesterday’s value plot:
Here’s today’s value plot:
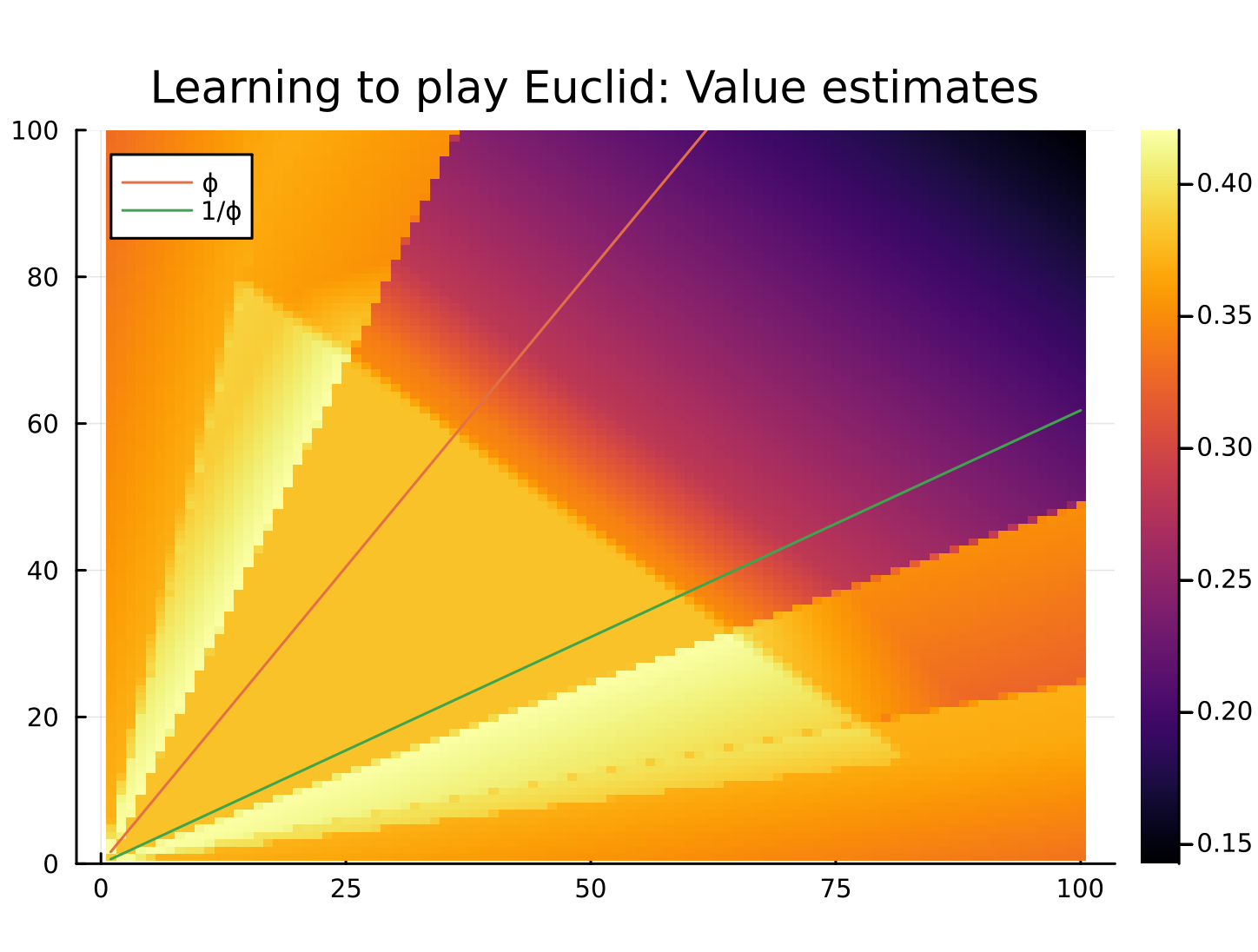
Optimal Euclid means player 1 should win when the larger value divided by the smaller value is an integer or is greater than the golden ratio, and player 2 otherwise. So the dark triangle forming between \(\phi\) and \(1/\phi\) was a good sign. Today’s plot definitely shows the effects of masking (I only allow actions of choosing multiplier 1 - 10 right now), which is no issue, but the positive glow in that inner triangle is giving me pause. I’m not sure if I introduced some error somewhere or if we’re learning. We’ll see, I guess.
RL/Alphazero ref dump:
- A Simple Alpha(Go) Zero Tutorial
- AlphaZero.jl
- Original AlphaZero paper
- Acquisition of Chess Knowledge in AlphaZero
- Impartial Games: A Challenge for Reinforcement Learning
- Minimal and Clean Reinforcement Learning Examples
- Reinforcement learning on the combinatorial game of Nim
Combinatorial game ref dump:
- Some Problems in Combinatorial Game Theory
- A Game Based on the Euclidean Algorithm and A Winning Strategy for it
- Properties of a Game Based on Euclid’s Algorithm
Julia ref dump: